Como funciona?
1
Pesquise diretamente pela barra de busca abaixo ou filtre as questões escolhendo segmento, disciplina, assunto, tipo de avaliação, ano e/ou competência.

2
Clique no botão [+] abaixo da questão que deseja adicionar a sua prova, ou arraste a questão para o organizador de prova.

3
Use a aba do organizador para excluir ou adicionar as questões de nosso banco para a sua prova.

4
Quando estiver satisfeito com montagem realizada, clique em “Prévia da prova” para visualizar sua prova completa.

5
Se quiser retornar para editar algo clique em “Editar prova”. Caso esteja satisfeito, insira seu nome e e-mail nos campos e clique em “ Finalizar”.

6
Basta acessar os links da prova e gabarito que serão exibidos!
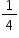 com alimentação,
com alimentação, 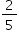 com aluguel e R$ 300,00 com transporte; ele deseja ainda que lhe sobrem, no mínimo, R$ 750,00. Para que suas pretensões sejam atendidas, o seu salário deverá ser no mínimo de:
com aluguel e R$ 300,00 com transporte; ele deseja ainda que lhe sobrem, no mínimo, R$ 750,00. Para que suas pretensões sejam atendidas, o seu salário deverá ser no mínimo de: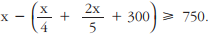
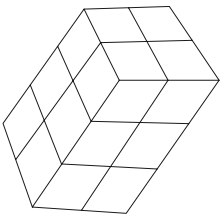 MILLINGTON, Jon. Petiscos matemáticos: ideias interessantes para
ocupar os momentos de lazer. Lisboa: Replicação, 2003. p. 27. Adaptado.
MILLINGTON, Jon. Petiscos matemáticos: ideias interessantes para
ocupar os momentos de lazer. Lisboa: Replicação, 2003. p. 27. Adaptado.







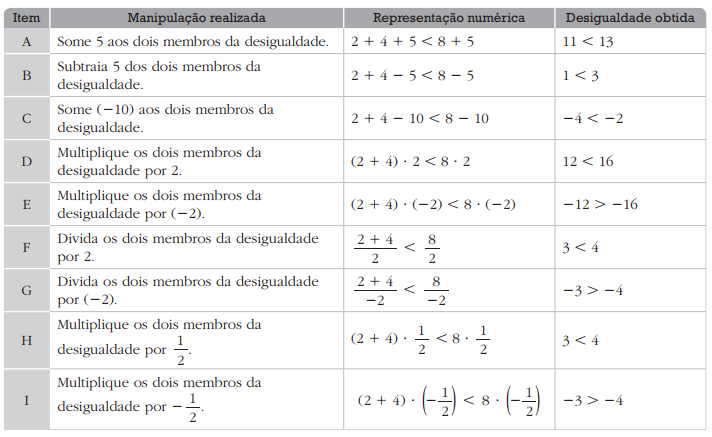
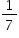 de aha dá 19.
de aha dá 19.

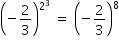 → portanto, a sentença é falsa.
→ portanto, a sentença é falsa.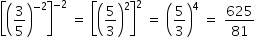 → portanto, a sentença é verdadeira.
→ portanto, a sentença é verdadeira.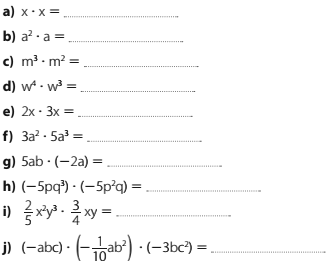
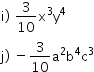


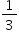 da população mundial apresentar sobrepeso ou obesidade enquanto cerca de
da população mundial apresentar sobrepeso ou obesidade enquanto cerca de 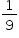 da população está desnutrida ou passa fome?
da população está desnutrida ou passa fome?