Como funciona?
1
Pesquise diretamente pela barra de busca abaixo ou filtre as questões escolhendo segmento, disciplina, assunto, tipo de avaliação, ano e/ou competência.

2
Clique no botão [+] abaixo da questão que deseja adicionar a sua prova, ou arraste a questão para o organizador de prova.

3
Use a aba do organizador para excluir ou adicionar as questões de nosso banco para a sua prova.

4
Quando estiver satisfeito com montagem realizada, clique em “Prévia da prova” para visualizar sua prova completa.

5
Se quiser retornar para editar algo clique em “Editar prova”. Caso esteja satisfeito, insira seu nome e e-mail nos campos e clique em “ Finalizar”.

6
Basta acessar os links da prova e gabarito que serão exibidos!

















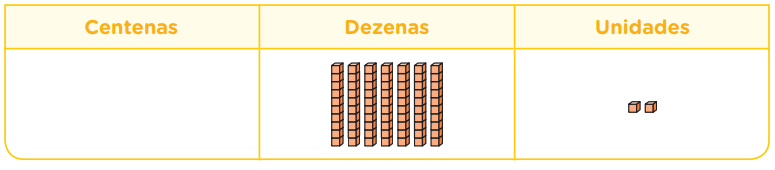
 nos dados. O que Elaine terá de fazer com os pontos que tirou?
nos dados. O que Elaine terá de fazer com os pontos que tirou? nos dados. O que Felipe deverá fazer para retirar os pontos que tirou nos dados?
nos dados. O que Felipe deverá fazer para retirar os pontos que tirou nos dados?

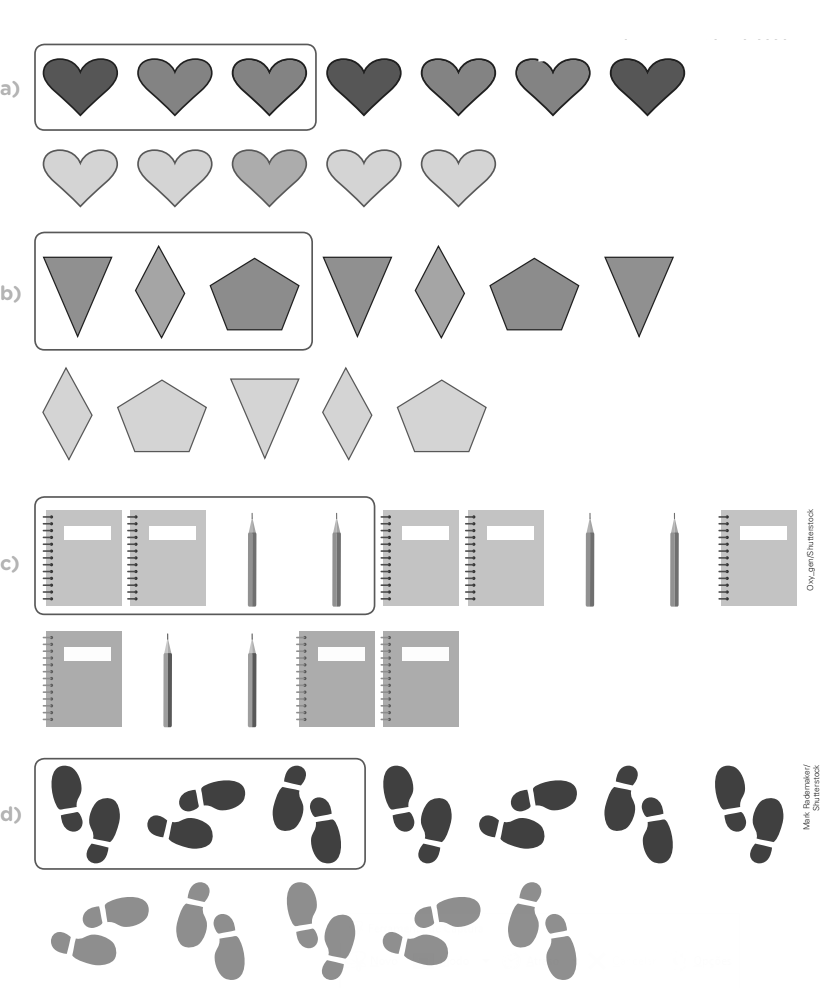

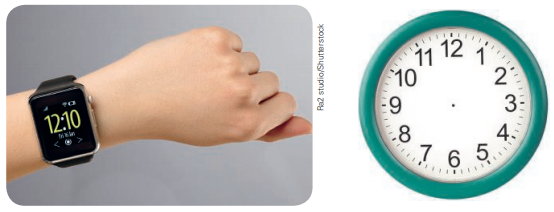


 Período da noite.
Período da noite. Período da tarde.
Período da tarde. Período da tarde.
Período da tarde. Período da manhã.
Período da manhã.